We live in a time of immediacy, where our desires are quickly fulfilled. Rapid turnover of inventory in stores minimizes the risk of shortages, ensuring people can obtain the items they require promptly. Additionally, sophisticated distribution networks enable deliveries within hours or days. A key element in orchestrating the timing and content of different network systems is the management of queues which govern the flow of goods. Techniques like Discrete Event Simulation (DES) help us model the multiple elements and sources of variance that are typical of these type of systems and deliver reliable recommendations. Moreover, we have great software which simplify this analysis. Regardless of this, the modeler needs to be familiar with the various complexities involved in using DES for the analysis of queueing systems some of which I cover below.
Queues and queueing systems
A queueing system is essentially any setup where individuals may wait in line due to competition for limited resources, a scenario ubiquitous in various settings. Examples include waiting for a cashier at a grocery store, a bank teller, or an ATM, as well as the wait for manufacturing subassemblies or in call centers and communication systems. The following figure illustrates the configuration of a simple queueing system:
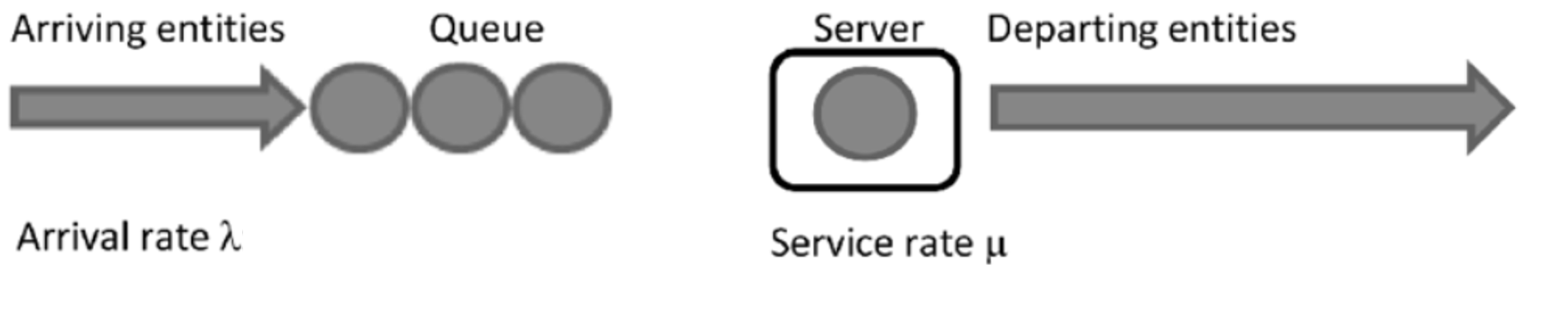
Queuing theory was developed at the start of the XX century to model queues. Techniques in this domain draw from probability, stochastic processes, systems theory, differential equations, and calculus. To standardize the description of queues, Kendall developed a notation with five fields: AP/ST/NS/Cap/SD where AP denotes the arrival process, ST the service time, NS the number of servers, Cap the maximum number of customers in the whole system and SD the service discipline or service order such as first come first served (FCFS) or last come first served (LCFS). In general, Cap is assumed to be infinite and SD is FCFS by default and can be omitted unless otherwise. So, in the case of the most simple and popular queue type, the M/M/1 queue, the arrivals follow a Poisson distribution, service times are exponentially distributed and there is one server. Also, we use M as this stands for memoryless or Markovian (a property shared by exponential and Poisson distributions). What are good examples of this type of system?
Here, I will demonstrate the analysis of a typical queuing system (a call center) using Discrete Event Simulation (DES) simulation. I will emphasize the main steps involved in a typical simulation analysis as well as some of the considerations that need to be considered to ensure the validity of results. In specific, I will focus on (1) the importance of common random numbers and (2) Comparing manual estimations obtained through Little’s law with those obtained through the simulation model.
Problem Description
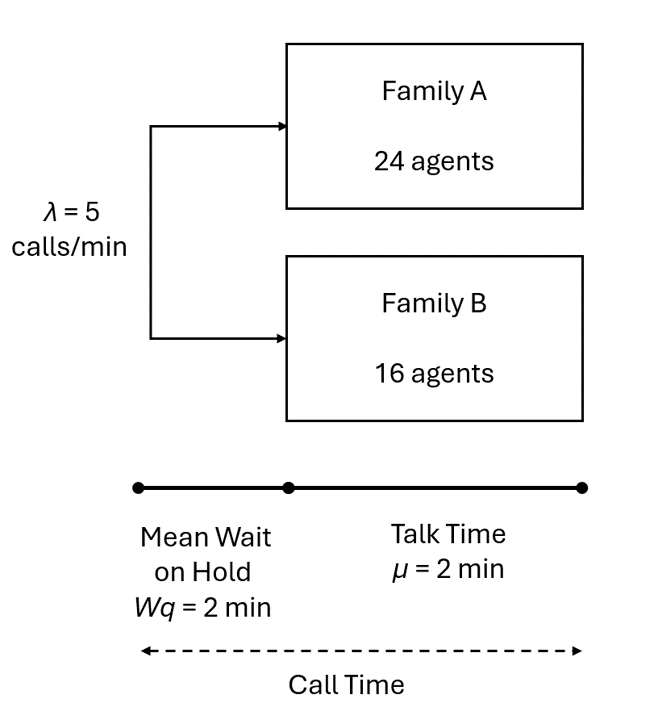
A hypothetical company, YX Corp operates a call center where customer service agents wait for incoming calls and then help the callers solve their computer software problems. The center handles questions about two families of software products. Customers have complained that during busy times they spend too much time waiting on hold, so YCC wants to look at system performance during the two hours of the day when demand is highest.
The call center helps customers solve their doubts about two different software products (product family A and product family B). Calls arrive at a rate of 5 calls per minute. 60% of callers have a questions pertaining to product family A, whereas, 40% of the callers have a question pertaining to product family B. In the current system, there are 24 agents trained to answer questions regarding product family A, and 16 agents trained for product family B. The routing system sends calls to the first available agent according to which product family the customer is inquiring about. Customers are willing to wait on hold before hanging up after a time period measured to be exponentially distributed with a mean of 2 minutes. The average “talk time” per customer is exponentially distributed with a mean of 8 minutes. The following is a graphical representation of the system:
YCC Corp uses the following measurements to track the performance of their service:
- Percent of calls that are answered or abandoned in 1 minute or less
- Percent of callers who abandon service
- Average time waiting on hold (for answered calls only)
- Utilization of agents
The first KPI is called the Telephone Service Factor (TSF). For YCC, TSF is the most critical performance measure and management needs to improve it. YCC Corp is considering the implementation of a modified system in an effort to improve their performance measures. The proposed system would require cross-training 10 of the 40 agents, to enable them to answer calls from either product family. The routing logic in this modified system will prefer dedicated agents over cross-trained agents to take calls from arriving customers, because cross trained agents are estimated to take 10% longer to answer questions. For customers waiting on hold, the first available agent will be assigned (whether dedicated or not), and if all agents are busy, the callers will wait in queues dedicated to their product family question.
Objectives
The following list details the objectives of this analysis:
- Develop an accurate baseline simulation model of the system, in which there are only agents dedicated to one of the two product families.
- Develop an accurate alternative simulation model which incorporates the inclusion of 10 cross-trained agents.
- Collect the KPIs of interest for each model
- Perform a comparative analysis to understand if the use of cross-trained agents improves the performance of the KPIs.
- Provide a recommendation to YCC Corp indicating if the cross-trained agents will improve the system performance.
Assumptions: For now let’s assume that the 10 cross-trained agents will be comprised of 6 agents from product family A, and 4 agents from product family B. This will result in a reduction from the dedicated agent staffing levels of product family A and B, respectively. Also, in our system workers have no other duties, they do not take breaks and there is no limit to the number of customers on hold.
Manual approximation
Before engaging in simulation, it is always a good idea to approximate manually the expected outcome for our models. In this case, as you may have noticed, we are solving an M/M/2 queue system and are interested in comparing two alternatives: (a) Our baseline model and (b) our modified model, which includes the cross trained agents. We will use Little’s Law to make our initial estimation.
A brief on Little’s Law: Little’s law (L = λW), also called a conservation law, relates waiting time to queue length in systems where arrivals are tied to rate λ. It explains the relationships between the key parameters and performance measures of this system when operating in the long- run or in steady state (i.e. when customer flows are stable). This law states that the average number of customers in the system at any arbitrary point in time, both in queue and in service, L, is equal to the average time spent in the system which results from multiplying the average number of customers that enter the queueing system per unit time (λ), and the average total time in the system (W). Here, we note that in a finite system we only care about those customers that “enter” the system excluding those that were turned away. From a practical standpoint, if the queue has a finite capacity but that capacity is seldom reached, it’s reasonable to approximate the problem as an infinite capacity problem. Also, note that finite queues are always stable. It holds for almost all queueing systems or subsystems regardless of the number of servers, the queue discipline, or any other special circumstances.
Little’s law represents a balance-of-flow relationship and applies to many situations. Here are some examples:
Table 1. Examples of using Little’s law in different business settings.
| System | L | λ | W |
|---|---|---|---|
| Retail Store | Total number of customers waiting in line | Rate of flow of customers from the moment they entered the queue until they left | Mean total time spent in the system |
| Traffic | Total number of vehicles waiting to access a highway | Rate of flow of vehicles as they enter and cross the highway | Mean total time a vehicle spends froom the moment it joined the X until it left the highway |
| Hydropower | Volume of water behind a dam feeding the hydropower system | Rate of flow of water from the dam into the hydropower system | Mean time a random water molecule spends in the system (both since entering and until traversing the exit of the dam) |
Depending on the type of queue system, the basic Little’s law equality will change. Also, more relationships can be established with respect to other system metrics. For instance, in a M/M/c system, we can estimate utilization for each server as follows:
So, this is what we get by Little’s law for our two server system:
Table 2. Initial estimation of agent utilization for current scenario.
| Agents A | Agents B | |||
|---|---|---|---|---|
| 5 * 0.6= 3 | 5*0.4 = 2 | |||
| 24 | 16 | |||
| 1/8 | 1/8 | |||
| 3/(24/8) = 1.0 | 2/(16/8) = 1.0 |
(For doubts about these estimations, go here!)
The queue calculations suggested that 3 customers will inquire for agents A and 2 for agents B. At a service rate of 1/8 customers per minute the utilization of both servers will be 100%. So, indeed, we are exceeding the system capacity and customer complains make sense. What is the expected improvement after cross-training ten agents?
Modeling approach
To analyze this queueing system we used SIMIO software (add note on why). Our logic for the baseline model involved first routing callers (i.e. customers) into “routing servers” based on caller type. From here, callers are sent to the appropriate agent based on availability. We used zero capacity input buffers for each agent server creating a “blocking” environment in the system, representing callers waiting on hold for the next available agent.
For the modified version, we checked first availability from the dedicated agent pool. If no dedicated agents are available, then we checked on a third pool of cross trained agents. When no agent is available, the caller waits, blocking other callers of that type from receiving service.
Also, a state variable is created to record the caller’s waiting time and allow exiting the system when this time exceeds their tolerance level.
Key Performance Indicator Tracking
Simio allows the creation of state variables to aid in the process of tracking KPIs. These variables were updated with add-on processes to assign values at the entity and system level.
- The “Assign Time Waiting” process, records the time a caller has waited before either abandoning the service, or reaching an agent. This process is assigned just before the caller is ready to be routed to an agent. Besides its use to determine if a caller will abandon, as described above, this assignment helps with the collection of statistics for the TSF, the percent of callers who abandon, and the average time waiting on hold for answered calls performance measurements.
- The “CountNumberServedOrAbandonedUnderOneMin” is responsible for tracking the number of customers who either receive services or abandon the system in less than one minute. This process will allow for the collection of statistics on the Telephone Service Factor (KPI#1). The process first determines if the warm-up period is complete (so no counts are recorded during the warm-up period). It then determines if the entity waited less than one minute. If the wait time was less than one minute, the TSF counter is incremented by one. This process is called every time an entity enters either the “AbandonSink” module or an agent’s server module.
- The “Sink1_Entered CollectTimeOnHoldForCallsAnswered” Process manages a variable which tracks the time a caller waited if their call ends up being answered by an agent (KPI #3). Each time a caller processes through the “Sink]” module, their corresponding wait time variable is recorded to allow for the model to track the average over the two hour analysis period.
Verification
Several methods were used for the verification of both the baseline and modified system models. The first method of verification involved a brief queuing analysis to compare expected utilization with that of the simulation’s measure of agent utilization. This was performed for agents A and B on the baseline model.
The queuing calculations suggested we should see about 100% utilization for agents A and B (Table 2). In comparison, the baseline model reported 90% and 91% average utilization for agents A and B, respectively. This suggests that our system is running at or close to expected with regards to agent utilization (considering that the estimations made are long term and that we are running our systems for only 2 hours).
Note: To allow for the performance measurements to represent the system at peak service times, servers were made busy at initialization. Alternatively, a simple
warm-up analysiscould be used. For instance, by tracking the combined utilization of the agents through a status box. Check how long it takes to reach steady state (something above 70% utilization) and exclude that from the analysis.
Building and testing every piece of logic. Verification also involved checking the animation itself, status boxes, breakpoints, and tracing tools and running the model with constant values to check performance without variability helps identify potential modeling issues. Moreover, we still need to make sure that our models are comparable (i.e. that the only or main source of variation is related to the modifications we want to test. For that we need common random numbers.
Note on Verification and Validation in DES Simulation: Verification and validation are two essential steps when running simulation analyses. Verification we ask if the computer model was correctly implemented. In Validation we ask if the model is an accurate representation of reality. In Verification we need to ensure that In Validation we want to ensure that the predicted performance is sufficiently close to actual system performance
Common Random Numbers (CRNs)
The use of CRN in simulation is essential, first, it ensures we generate iid (independent and identically) distributed arrival and service times which is a key assumption made by most queueing models. Second, it allows us to compare systems by ensuring that everything is similar except the change we are testing. In other words, it controls for all the sources of randomness that could bring noise to the model.
For this problem, we assigned the same random stream numbers in each model at the following places:
- Arrival rate of callers
- Assignment of caller type (product family A or B)
- Time willing to wait (upon creation of each entity)
- Processing time for each caller (upon creation of each entity)
By incorporating CRNs we should be able to see a reduction in variance across replications. This will effectively reduce the half-width around the true mean when calculating our confidence intervals (i.e. a better estimate of our true mean). Tables 3 and 4 summarize the results obtained with and without CRNs (please see the Appendix to find the formulas used in each case.)
Table 3. Key parameters and confidence intervals on the difference between correlated systems (CRNs being used).
| KPI | D-bar | Std Deviation | Lower Bound | Upper Bound | Conclusion (Winner) |
|---|---|---|---|---|---|
| TSF | 0.0357 | 0.0073 | 0.0138 | 0.0472 | Current system |
| % Callers abandoning | -0.0357 | 0.0059 | -0.0494 | -0.0223 | New system |
| Avg. time on hold | -0.0007 | 0.0001 | -0.0011 | -0.0003 | New system |
| Agent utilization | -0.0250 | 0.0130 | -0.0544 | 0.0044 | Indifferent |
Table 4. Key parameters and confidence intervals on the difference between independent systems (CRNs not being used).
| KPI | Y1_bar - Y2_bar | Lower Bound | Upper Bound | Conclusion (Winner) |
|---|---|---|---|---|
| TSF | 0.0721 | 0.0317 | 0.1126 | Current system |
| % Callers abandoning | -0.0908 | -0.0289 | New system | |
| Avg. time on hold | -0.0025 | -0.0008 | New system | |
| Agent utilization | -0.0669 | 0.0519 | Indifferent |
Notice that conclusions about the winning model do not change regardless of whether we use CRNs or not. However, look at the width of the confidence intervals:
Table 5. Confidence interval width when not using CRNs and when using them.
| KPI | No CRNs | CRNs |
|---|---|---|
| TSF | 0.0808 | 0.0334 |
| % Callers abandoning | 0.0619 | 0.0271 |
| Avg Time on Hold | 0.0016 | 0.0008 |
| Agent Utilization | 0.1189 | 0.0589 |
As demonstrated here, the reason why we want to use CRNs in simulation analysis is because it decreases noise due to randomness and allows us to focus on the actual impact on the different KPIs. With CRNs we obtained better point estimates.
Interpretation of results and recommendations
The initial question of YCC was whether by cross training ten operators they could decrease customer complaints regarding long waiting times at peak hours.
When looking at the results with CRNs. We observe that the difference of the current system with respect to the new system can be quite remarkable (3.2% - 11.3%) in terms of % of calls answered or abandoned within one minute or less (TSF). When looking at the overall % of callers abandoning the system (at any point) we observe a difference of between 5% to 2.2% less in the new system. The other two metrics show differences that are quite close to zero or include zero (in the case of agent utilization) which implies that although there is statistical difference between the two systems, practically, such difference may not be of great importance.
Therefore, it seems like investing in the cross-training of ten agents will not represent a remarkable advantage for the manager. The next step could involve running more experiments to guarantee that there is little or no practical evidence of improvement or testing an alternative modification to the system (e.g. adding more agents). As a note of caution, it is always important to remember that these results are valid for the current system configuration (arrival times, processing times, customer willingness to wait, etc.). If there was a change in, for example, the demand rate our results may look different. So, it is important to consider potential changes in system configuration from the beginning to guarantee the validity of results for a reasonable period of time.
===
Overview of steps involved in DES
The main purpose of this article is to provide with an overview of the various steps involved in running a solid simulation analysis. Unfortunately, it is impossible to cover every aspect of this process. However, here are a few highlights:
Main Steps to Carry a Simulation Analysis:
- Formulation of a model of the process or problem under study.
- Define problem, objectives and assumptions.
- Define problem, objectives and assumptions.
- Choosing a strategy to be evaluated, or equivalently, designing a set of experiments to be carried out using the model.
- Define what changes will be implemented in the system.
- Estimate expected behavior.
- Specify verification and validation techniques to be used.
- Define what changes will be implemented in the system.
- Carrying out these experiments and recording the model’s behavior under the experimental conditions.
- Ensure the model captures the actual behavior you want to test (e.g. initialization vs steady-state).
- Ensure similarity of modified models in everything except the factors being tested (CRNs).
- Collect model outputs.
- Ensure the model captures the actual behavior you want to test (e.g. initialization vs steady-state).
- Analyzing the results of these experiments, making some judgements about how the real situation would behave under the experimental conditions and formulating a plan of action.
- Compare new models vs baseline model.
- Determine practicality of results.
- Define next steps.
- Compare new models vs baseline model.
Additional tips:
- Use good programming skills:
- build and test one piece of logic at a time.
- find errors before they propagate (build & test).
- find errors before they propagate (build & test).
- document the model with thorough comments.
- define every variable precisely.
- describe the purpose of each step of logic.
- define every variable precisely.
- build and test one piece of logic at a time.
- Examine the output for reasonableness.
- try different parameter values.
- try different parameter values.
- Trace (display) all events and system status.
Appendix
Table A.1. Formulas to compute confidence intervals on the difference of correlated data.
| {r = 1}^{R} D{r} | |
| {r = 1}^{R}(D{r} - )^{2} | |
Table A.2. Formulas to compute confidence intervals on the difference of two independent data sets.
| θ{2} = Y{1} - Y_{2} | |
|---|---|
| {r = 1}^{R}(Y{ri} - )^{2} | |