What is Optimization? (continuation)

Here we will cover the remaining steps in the development and deployment of optimization models:

  3. Choose an appropriate solver and modeling environment.  
  4. Model building or development.  
  5. Solve the model.  
  6. Analyze the solution.  
  7. Model validation and sensitivity analysis.  
  8. Report results and make decisions.  
  9. Iterate, improve and scale.

3. Choose an appropriate solver and modeling environment

Deciding what math model to use for a specific problem is the core job of the modeler. Besides this, once the optimization problem is properly formulated as a math problem, we need to identify an adequate METHOD to SOLVE it. In other words, we need to identify a method that will help us choose the values that our decision variables need to take to achieve the optimal objective. The solution algorithms used mostly vary according to the types of models indicated above:

The simplex and the interior point methods are the prominent procedures used to solve linear programming problems.
Branch and bound is widely used for integer and mixed-integer programming.
The solution to nonlinear programming problems is obtained either through the so-called descent_ algorithms (steepest descent, Newton method, penalty barrier methods and feasible direction methods), probabilistic meta-algorithms such as simulated annealing or heuristic strategies like local search or particle swarm optimization.
The solving methods used for MCMP require input from the decision maker in some way or another. Therefore, we have methods:
1. where the DM provides complete information about the preference function,
2. where no information is available and
3. where partial information is available.
  Goal programming, compromise programming and interactive programming methods fall into categories (1), (2) & (3), respectively.

Luckily, there are software tools that automate the process of implementing these different algorithms. Thus, the primary tasks for the modeler when solving an optimization problem involve two steps:

Select a Solver: Choose a solver that fits the problem type (e.g., Gurobi, CPLEX for LP/MIP; KNITRO for NLP).
Decide on a Modeling Tool: Choose a modeling environment (e.g., GurobiPy for Python, AMPL, GAMS).

Mathematical optimization solvers today automate the application of algorithms. Therefore, the user does not “see” or “manualy solves” the optimization model (much like what happens with machine learning models) since optimization solvers are software tools designed to find the optimal solution to mathematical optimization problems. They can handle various types of optimization problems, including linear programming (LP), mixed-integer programming (MIP), nonlinear programming (NLP), and more. Some of the major optimization solvers widely used in academia and industry include commercial solvers such as CPLEX, Gurobi, MOSEK and KNITRO or free, open-source, solvers like CBC, SCIP, GLOP and COIN-OR.
The modeling environment includes optimization libraries and toolkits that integrate various solvers and are now available through major programming platforms such as Python (SciPy, Pyomo, PuLP, CVXOPT, etc.), R (optim, ROI, lpsolve, etc.), MATLAB, C and others. These libraries offer some model building capabilities as well as open-source solvers by default or access to the most advanced solvers through a purchased license.
In addition, there are commercial standalone optimization software companies which for a long time have focused on making solvers more accessible to the modeler and on streamlining the entire optimization process. These companies offer an algebraic modeling language which is meant to simplify the writing of models as well as sophisticated Integrated Development Environments (IDEs) that facilitate model running, debugging and output review. GAMS, AMPL, and Lindo have been established in the market for a long time, alongside IBM ILOG CPLEX Optimization Studio.
In third term, we have specialized companies which have focused on customizing optimization solutions to address specific market or business problems. AIMMS, for instance, has developed an extremely friendly user interface which makes it easier for business users to build and implement models quickly.

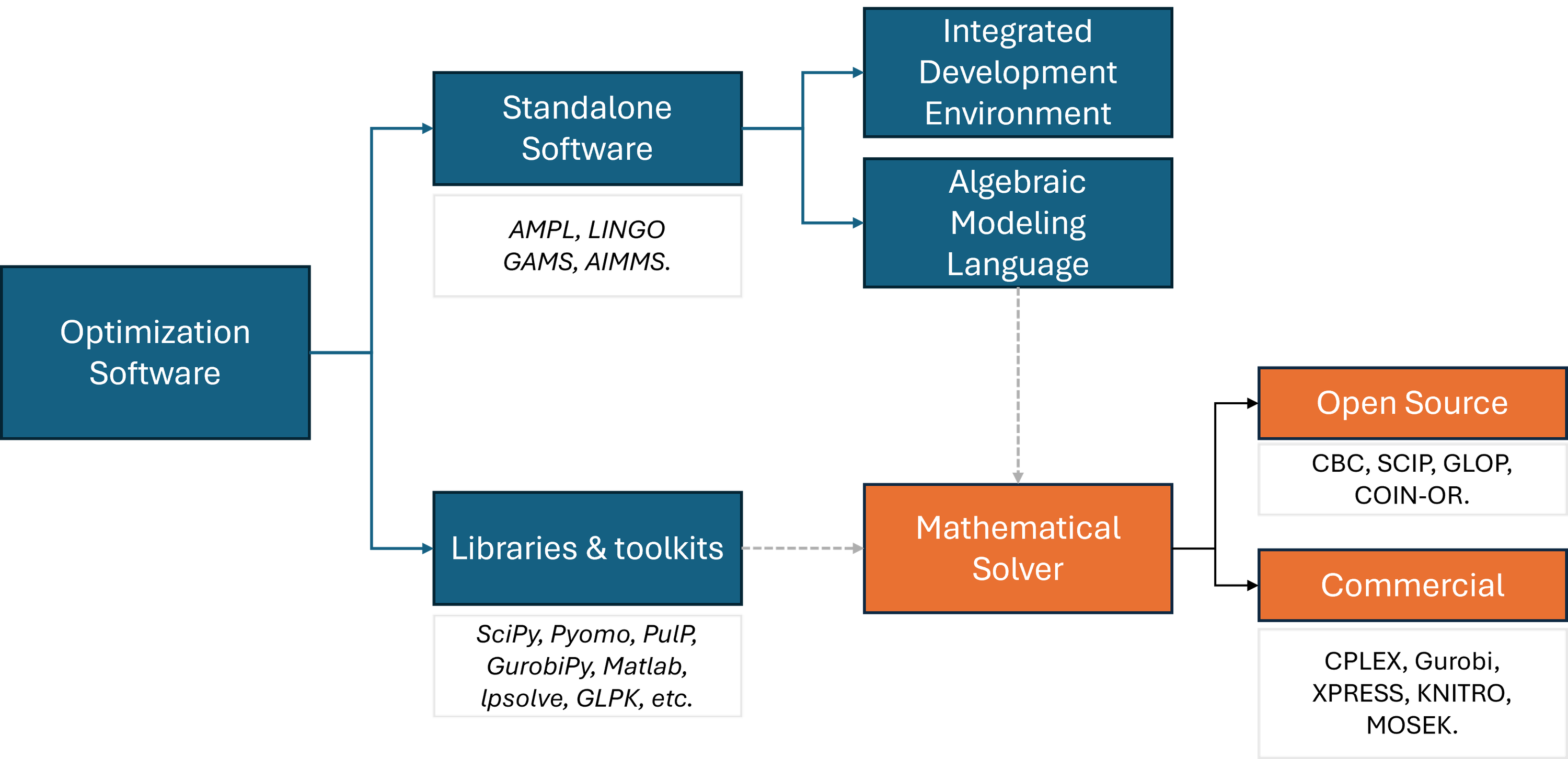
Figure 1: Optimization Software Ecosystem

Also, recently, the optimization ecosystem has been enhanced by operational frameworks similar to those being adopted for machine learning. Nextmv, for instance, is a DecisionOps framework that focuses on streamlining the to build, test, deploy, and scale steps for quickly deploying decision models to production, maintaining and monitoring them. Just as MLOps, it facilitates collaboration among decision scientists, Data engineers, IT professionals, and others.

The most advanced optimization software enables efficient problem handling and solution. Check INFORM’s Optimization Software Survey Results for a list of major open source and commercial software along with their key features.

4. Model building or development.

Once the model was formulated as a matematical model and the decision was made about what solver and modeling environment to use, the next step includes:

Setting Up the Environment: Install necessary software and libraries.
Coding the Model: Implement the mathematical model using the chosen tool. Define variables, objective function, and constraints. Read the input data and define how outputs will be read.

For a beginner’s introduction to optimization modeling, consider checking out the latest course released by Gurobi on Udemy. They cover the process of translating a problem from its basic form into a mathematical model and then into a computational model.

5. Solve the model

Run the Solver: Use the solver to find the optimal solution.
Check Solver Output: Ensure that the solver has converged to a solution and examine the solution status.

Issues raised when solving optimization problems
There are various issues that can emerge when solving optimization problems. Some of the most common are:

Infeasibility occurs when the optimization problem has no feasible solution that satisfies all constraints.
Degeneracy refers to a situation where multiple variables have the same value in the optimal solution.
Unbounded Solutions when the objective function can be increased (for maximization) or decreased (for minimization) indefinitely without violating any constraints.
Slow Convergence is when the algorithm takes an excessive number of iterations or time to converge to an optimal solution.

6. Analyze the solution

This phase involves reviewing the results and ensuring that they make sense. For this, extract the optimal values of the decision variables and interpret them in the context of the original problem.

7. Model validation and sensitivity analysis

Now that the model is working properly, let’s dig further and ensure that it is equiparable to an existing or potentially real model. Also, ensure, we leverage the expertise of someone unfamiliar with the development proces.

Validate the Model: Compare the model results with known benchmarks or real-world data.
Perform Sensitivity Analysis: Understand the robustness of the model by analyzing how changes in input data affect the the cost of your optimal plan. Alternatively, you can run a wide range of scenarios and compare the optimal plans for each to understand how optimal decisions might vary with different data.
Get backup from a third party: Someone not involved in building the model should certify that your claims about performance under different scenarios are well grounded.

8. Report results and make decisions

Document Findings: Prepare a report summarizing the problem, model, solution, and insights. Include time to payback (TTP) as the single most important metric of performance.
Implement Decisions: Embed the model within the company at a low scale. Use the optimization results to inform decision-making processes in the relevant domain. Leverage stakeholder support.

9. Iterate, improve and scale

Refine the Model: Based on feedback and new data, refine and improve the model.
Continuous Improvement: Continuously monitor the model’s performance and update it as needed to maintain its relevance and accuracy.
Show adoption and results: Demonstrate before and after performance at different sites or locations.
Educate people and create enthusiasm: Train and certificate people and change the conversation around what is possible vs what is failing. Build field and top management support.
Install across the enterprise: Create a consistent pipeline. Reward and expand team.

In forthcoming publications, I’ll be exploring many of these techniques. So, stay tuned!

Bibliography & resources:

Bertsimas, Dimitris and Robert M. Freund (2004) Data, Model, and Decisions. The Fundamentals of Management Science. Dynamic Ideas.530 p.
Gurobi on Udemy
Guenin J. et al. (2015) A gentle Introduction to Optimization. Cambridge University Press. 269 p.

What is optimization - part 1