Revenue management, or RM, encompasses a set of strategies and tactics employed by firms to systematically regulate demand for their offerings. This field has garnered considerable attention recently, emerging as one of the most successful application domains within Operations Research (OR). Originating as a niche practice primarily adopted by a few major airlines following deregulation in the United States around 1978, revenue management has evolved into a widely adopted business approach. Its application today extends across various industries, with notable users in the car and hotel booking industries. The economic significance of revenue management cannot be overstated, with reported revenue increases of 5% (Ryzin and Talluri 2005) or more across multiple industry implementations of RM systems. Both professional practice and scholarly research in this field are expanding rapidly. Annual industry conferences dedicated to
revenue management now abound, while scholarly publications focusing on RM methodologies are experiencing rapid growth. Here I will introduce the use of optimization to solve a basic Revenue Management problem using an example from the hotel industry and drawing on excerpts from various sources.
Hotels implement different types of controls to maximize revenue. On one side they have an ascending scale of rate classes, separated by rate fences, or restrictions that make a particular rate available to one segment of customers but not to another. Daily forecasted demand is used to determine what rate classes are open or closed each day. Through the length of stay control customers are further segmented by the number of days they wish to stay in the property.
Revenue Management Systems decide which combinations of rate class and length-of-stay to declare open. Bid pricing is the technique used for this purpose. A control price is estimated for each day of the planning horizon, this is referred as bid price and it represents the marginal revenue the hotel would receive if it were to increase its capacity on that date by one room.
If the hotel is not forecasted to sell out, the bid price is zero since increasing the capacity will not increase the revenue. In this case all rate classes are open and it should sell any room it can. When the demand forecast exceeds capacity, the bid price will be greater than zero, and some of the rates may be closed. For multiple-night-stays, a typical approach is to average the bid prices for the dates involved. Rate classes above the bid price are open, and others are closed.
NOTE: The demand forecast must be of arrivals, as opposed to occupied rooms, and will be segmented by rate class and length-of-stay. For large hotels similar rate classes may be aggregated into similar rate buckets and the revenue management system will declare certain buckets to be open or closed. This demand forecast is, also, unconstrained meaning it excludes any limit imposed by capacity but considers all the potential arrivals on any given date. In the following simple example we assume a pre-determined and static pricing structure while in a real scenario dynamic pricing structures may be applied to the same room to improve market share.
A toy example
For illustrative purposes, let’s say we have a property called the Revenue Inn. This property has 10 rooms, and offers a night rate of $129 for corporate clients and $99 for leisure clients. In this case, we assume that hotel guests don’t stay for more than 3 days and the planning horizon is one week. The demand forecast is given in the following tables:
Table 1: Demand Forecast for Corporate Clients
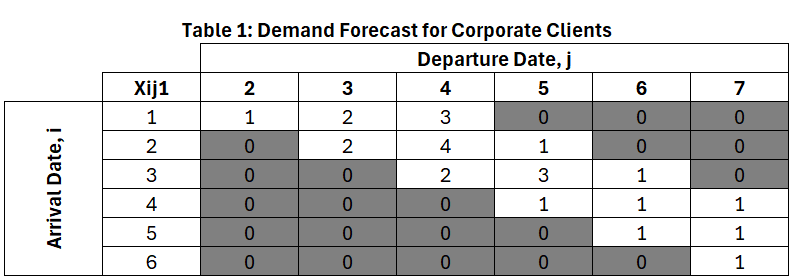
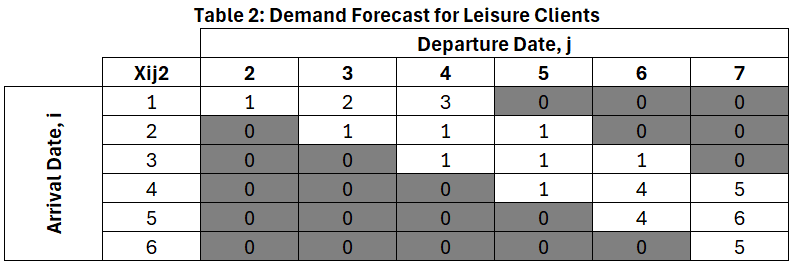
The main decision faced by the revenue manager is how many customers of each type to accept. In our revenue model we represent this decision through a set of decision variables which indicate the number of customers to accept who wish to arrive on day i, leave on day j, and pay rate class k. Therefore, we’ll observe arrivals 6 days a week and departures will start one day after the arrival day. Since we are planning for a weekly horizon the maximum departure day is 7. Also, remember, we have 2 rate classes.
Mathematically, we’ll have:
Model Formulation
Sets and Indices
: Index and set of arrival dates.
: Index and set of departure dates.
: Index and set of rate class.
Parameters
: Forecasted demand for arrival day , departure day and rate class .
: Total hotel capacity for leisure and corporate clients
RC = $129: Revenue from corporate clients (USD)
RL = $99: Revenue from leisure clients (USD)
Decision Variables
: Indicates the number of customers to accept who wish to arrive on date $i$, leave on day and pay rate class .
Objective Function
Total Revenue: Maximize total revenue.
Max {i=1}^I {j = i+1}^{min(i+3,7)} [x_{i,j,1} (j-i)RC + x_{i,j,2}(j-i)RL]
Constraints
(1) Meet forecasted demand: The number of reservations for a particular rate class $k$ and length of stay combination cannot be higher than the forecasted demand.
(2) Meet daily demand: Each day of the planning horizon, the total number of guests in the hotel cannot exceed the property’s capacity. Notice that for days 2 through 6 we consider the capacity used by customers arriving on that day plus that used by customers arriving on previous days who have not departed.
day 1 {j = 2}^{4} (x{i,j,1} + x_{i,j,2}) Hcap
day 2 {i = 1}^{2} {j = 3}^{i+3} (x_{i,j,1} + x_{i,j,2}) Hcap
day 3 {i = 1}^{3} {j = 4}^{i+3} (x_{i,j,1} + x_{i,j,2}) Hcap
day 4 {i = 2}^{4} {j = 5}^{i+3} (x_{i,j,1} + x_{i,j,2}) Hcap
day 5 {i = 3}^{5} {j = 6}^{i+3, 7} (x_{i,j,1} + x_{i,j,2}) Hcap
day 6 {i = 4}^{6} (x{i,7,1} + x_{i,7,2}) Hcap
(3) Non-negative room allocations
x_{i,j,k}> 0 i I; j J; k K
Solution
This problem was formulated as a linear program which means that both the objective and the constraints are expressed through linear equations. Here is the solution obtained by using Excel’s Solver (a good alternative for short problems like this one). According to this solution (see the values automatically filled in the Revenue Model sheet or those listed in the Answer Report), the optimal allocation for each day and customer type is as follows:
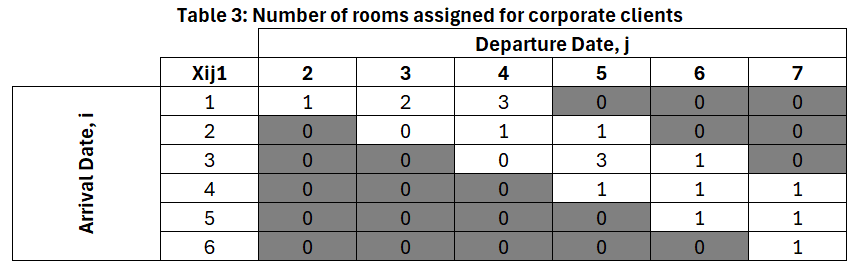
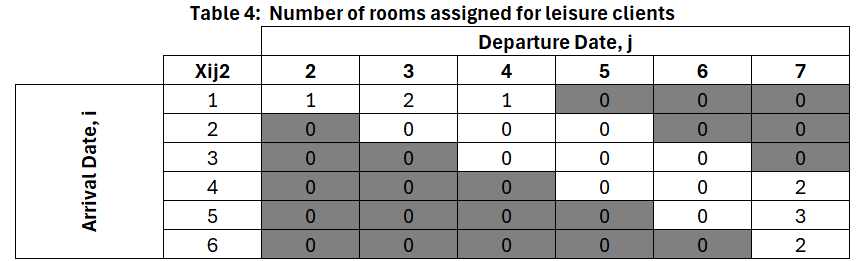
The total revenue achieved with this allocation is $7,080 (USD). Observe that with this solution we are making use of the maximum room capacity on each day.
Bid price
As said before, a control price bid price is estimated for each day of the planning horizon and it represents the marginal revenue the hotel would receive if it were to increase its capacity on that date by one room.
We can determine the bid price by looking at the shadow prices listed in the Sensitivity report. In technical terms, the shadow price of a constraint in a linear program is the increase in the optimal objective value per unit increase in the RHS of the constraint. In our case, our report indicates that, for our capacity constraints, per every increase of hotel capacity of one unit the total revenue will increase by $39 on day 1, $129 on days 2 and 3, and $99 on days 4, 5, and 6. If the hotel is not forecasted to sell out, the bid price is zero since increasing the capacity will not increase the revenue. In this case all rate classes are open and it should sell any room it can. When the demand forecast exceeds capacity, the bid price will be greater than zero, and some of the rates may be closed. For multiple-night-stays, a typical approach is to average the bid prices for the dates involved. Rate classes above the bid price are open, and others are
closed. So, if a customer arrives on day 1 and departs on day 3. The average bid price is $99, this implies that the rate class for corporate clients will be open on those days as the corporate rate of $129 is greater than $99. Alternatively, a room can be sold if the total payment for the corresponding stay exceeds the sum of the bid prices of the nights in the entire stay period.
Notice that a class for a booking is opened for sale if the fare associated with the (length of stay, class) pair exceeds its bid price. Otherwise, the class is closed. An advantage of the bid price method is that it takes into account the remaining capacity and open/closed pair (length of stay, class) status only. However, once a class is opened, there are no limits on the number of accepted requests. In order to control the selling process, the bid prices are refreshed periodically. Thus, some classes are closed and some classes are opened.
IMPORTANT: The Shadow Price of the i-th constraint is ONLY valid within the RHS range indicated for that constraint. For instance, the bid price for day 4 is $99 but only if total capacity is within 8 and 13 rooms. So, if we were to increase capacity by four units, a new estimation of the bid price needs to be obtained.
Other methods
Class control
For each night the class control method determines a certain amount of rooms that can be sold in each class. The amount of rooms in each class can be different for each night. For the entire stay which comprises several nights, the rooms of the same client must be of the same class for all nights. For example, a client can book tickets of class A on a stay comprising night 1 and night 2 only if A class tickets are available on both nights. Let us consider the case of two nights DAY1-DAY2 and DAY2-DAY3 and assume that each of them has only one empty room. There are only two customers willing to buy tickets. One client is willing to pay 70$ for class A in the stay of DAY1-DAY2 and the other client is willing to pay 210$ for class A in the stay of two nights DAY1-DAY2 and DAY2-DAY3. In the class control method, rooms are available only if the night and the class are both available at the same time. It is also impossible to block the 70$ request for the class A room while the 210$ class A room is still open for sale. The class control method does not control such cases and therefore loses opportunities to increase income.
Virtual nesting
The virtual nesting approach creates “virtual buckets” of stays based on the value rather than on the class. The approach creates value based virtual buckets on each night, and then requests for each night in each pair (length of stay, class) are assigned to these virtual buckets. Consider the example of two nights above. Say, two virtual buckets are created in this case: Bucket 1 is for high value requests, and Bucket 2 is for low value requests, see Table 5.
Table 5. Number of rooms in a virtual nesting approach.
| Buckets / Nights | Day 1 | Day 2 |
|---|---|---|
| Bucket 1 (high value) | 1 | 1 |
| Bucket 2 (low value) | 0 | 0 |
Rooms are made available in Bucket 1 on the tree nights. To block a low value request and make a high value request eligible, the method will assign the $70 Class A request on day 1 to Bucket 2 and the $210 Class A request on day 1 and day 2 to Bucket 1. Note that, if there are multiple fare requests, the process of assigning them to the buckets is not trivial.
The bid price method is similar to virtual nesting but it avoids complications with assigning requests for pairs (stay, class). A shadow price is linked to each night in the network and it represents a marginal lost from reducing the capacity of this night by one room. The bid price (value, opportunity cost of selling one room) of a pair (length of stay, class) in the network is equal to the sum of the shadow prices over the nights comprising the stay. A class for a stay is opened for sale if the fare associated with this pair (length of stay, class) exceeds its bid price. Otherwise, the class is closed.
Applications
Optimization models and methods are almost the same for hotels, airlines, car rentals and other companies. Therefore, the basic linear programming model illustrated above could be used to maximize the total income of other businesses too. Some equivalent notions in are given below.
Table 6. Equivalent RM notions across businesses. Source: Modified from (Bandalouski et al. 2018).
| Air transportation | Hotel business | Car rental business |
|---|---|---|
| Leg | Night | Day |
| Route | Period of stay | Period of rental |
| Class | Room type | Car type |
| Capacity of leg l | Number of rooms for night l | Number of cars for day l |
| Expected number of orders for the pair (route, class) | Expected number of bookings for the pair (period of stay, room type) | Expected number of bookings for the pair (period of stay, car type) |
| Price of one seat for the pair (route, class) | Price of one night for the pair (period of stay, room type) | Price of one day for the pair (period of stay, car type) |
In summary, we could say that RM is applied in any business where tactical demand management is important and the technology and management culture exists to implement it. Given this criteria, numerous industries present viable opportunities for revenue management. Nearly all businesses contend with fluctuations in demand, uncertainties, and diverse customer preferences. Additionally, many encounter constraints in their supply or production capabilities. Thanks in part to recent advancements in enterprise software and e-commerce, many companies have automated their operations, setting a favorable stage for the adoption of RM. Nonetheless, the feasibility of RM ultimately boils down to a cost-benefit evaluation specific to each firm. While for some, the potential advantages may not outweigh the implementation costs, it is likely that for the majority of enterprises, RM will eventually prove justifiable within their respective industries. The historical trajectory of RM in sectors like airlines, hotels, and retail indicates that once embraced, its adoption tends to spread quite rapidly. Therefore, it wouldn’t be surprising to witness RM systems (or analogous systems fulfilling RM functions under alternative labels) becoming as widespread as ERP, SCM, and CRM systems are today.(Ryzin and Talluri 2005)
+++
To dig deeper on this topic, you may find helpful the following resources: